Never-ending Games

News | Motivation | Topics | Time Schedule

Two-player games (of perfect information)

A two-player game is played by two players, for simplicity called Player 0 and Player 1, on a directed graph, called the arena. The nodes of the arena are split between the two players, i.e. every node belongs to either Player 0 or Player 1.

A play of the two players in the arena is formed by moving a pebble along the edges of the arena: Initially the pebble is located on some node v of the arena. The player who owns (or controlls) the node v, then moves the pebble along an edge of the arena to any successor of w he likes. Then it is the turn of the player who owns w to move the pebble in the same way to a successor of w. At every point of time, both players know exactly the states visited so far by the play. This is called perfect information. (For an example of imperfect information consider a game like poker.)

In general it is assumed that both players keep moving the pebble as long as possible. That is, a play is in general an infinite path v₀v₁v₂...v_iv_i+1... in the arena. A play is always won by exactly one of the two players, i.e. there are no draws.

The winner of an infinite play is decided by means of the winning condition. More precisely, the winning condition describes what plays are won by Player 0.

The most basic winning conditions are formulated by means of a subset F of nodes of the arena, e.g.:

• Player 0 wins a play if the play visits any node of F at least once. (Reachability game)
• Player 0 wins a play if the play visist nodes of F inifinitely often. (Büchi game)
• Player 0 wins a play if the play never visists nodes of F. (Safety game)

A node v is said to be won by Player 0 (Player 1) if he can react on the moves of his opponent in such a way that any resulting play (starting in v) is won by Player 0 (Player 1).

The central questions for these games are:

• Given a starting node v determine the player who wins v.
• Compute the subset of all nodes won by Player 0 (Player 1).
• Given a node v won by Player 0 (Player 1) compute a strategy for him that tells him how to react on the moves of his opponent so that any resulting play is won by Player 0 (Player 1).

These kind of games naturally arise e.g. in

• Controller synthesis: Given is a system which can be controlled by Player 0 and Player 1. Player 1 represents the adversarial environment. The winning condition describes the correct execution of the system. The goal is to compute a strategy (synthesize a controller) for Player 1 which ensure that the system operates correctly. For a simplistic example, see below.
• Model checking: Given is a system and a specification. Player 0 tries to show that the system satisfies the specification, while Player 1 tries to show that it doesn't.

Example: Safety games and controller synthesis

Two-player games as described above can be used to model the interaction of systems (e.g. given by means of a program) with their environment. Consider the following program fragment:

Here, only a very restricted interaction takes place, namley the input of a single character by the controller of the nuclear plant, while the environment has no real influence here.

The relevant question (which is obvious to answer in this case) is whether the controller can steer the system described by the program in such a way that the nuclear plant does not explode. And further, if he can do so, synthesize a correct program for the controller.

This question can be reformulated in terms of a safty game played on the configuration graph of the program.

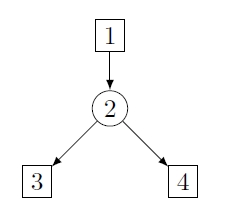
The graph itself is essentially the configuration graph of the program, i.e. the nodes correspond to the possible configurations (states) of the program. Circular nodes belong to the controller (Player 0) and rectangular nodes belong to the environment (Player 1).

The "good" program executions naturally give rise to the the winning condition, namely the safety condition which tells the user (Player 0) to never visit F = {3}.

The set of nodes won by Player 0 is obviously {1,2,4}, and he can win all of these nodes by using the strategy "In node 2, move the pebble to node 4" which can be translated into the code for the controller.

A more complex program might yield the following arena:



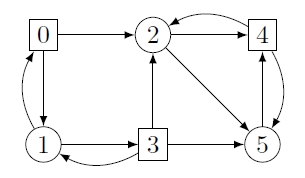
Again, the nodes of the controller (Player 0), resp. the environment (Player 1) are of circular, resp. rectangular shape.

Consider again as winning conidition the safety condition with F={3}, i.e. the controller has to ensure to never visit node 3 to win a play.

In this example, we see that the user has can win all nodes except for 3 by using the simple strategy "Always move the pebble from node 1 to node 0". (The choice of the controller in node 2 does not matter.)