Reference:

M. Luttenberger and M. Schlund. Convergence of Newton's Method over Commutative Semirings. Information and Computation, ?(?):??–??, To appear.

Abstract:

We give a lower bound on the speed at which Newton's method (as defined in (Esparza/Kiefer/Luttenberger, 2007)) converges over arbitrary -continuous commutative semirings. From this result, we deduce that Newton's method converges within a finite number of iterations over any semiring which is ``collapsed at some '' (i.e. 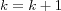holds) in the sense of (Bloom/Ésik, 2009). We apply these results to (1) obtain a generalization of Parikh's theorem, (2) compute the provenance of Datalog queries, and (3) analyze weighted pushdown systems. We further show how to compute Newton's method over any -continuous semiring by constructing a grammar unfolding w.r.t. ``tree dimension''. We review several concepts equivalent to tree dimension and prove a new relation to pathwidth.

Suggested BibTeX entry:

@article{LSInfComp15,
    author = {M. Luttenberger and M. Schlund},
    journal = {Information and Computation},
    number = {?},
    pages = {??--??},
    title = {Convergence of {N}ewton's {M}ethod over {C}ommutative {S}emirings},
    volume = {?},
    year = {To appear}
}