|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
Publications - On Rationality of Nonnegative Matrix Factorization
|
|
 |
|
 |
|
Reference:
Dmitry Chistikov, Stefan Kiefer, Ines Marusic, Mahsa Shirmohammadi, and James Worrell. On rationality of nonnegative matrix factorization. In Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 1290–1305. SIAM, 2017.
Abstract:
Nonnegative matrix factorization (NMF) is the problem of decomposing a given nonnegative 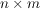 matrix M into a product of a nonnegative matrix M into a product of a nonnegative 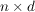 matrix W and a nonnegative matrix W and a nonnegative 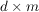 matrix H. NMF has a wide variety of applications, including bioinformatics, chemometrics, communication complexity, machine learning, polyhedral combinatorics, among many others. A longstanding open question, posed by Cohen and Rothblum in 1993, is whether every rational matrix M has an NMF with minimal d whose factors W and H are also rational. We answer this question negatively, by exhibiting a matrix M for which W and H require irrational entries. As an application of this result, we show that state minimization of labeled Markov chains can require the introduction of irrational transition probabilities. We complement these irrationality results with an NP-complete version of NMF for which rational numbers suffice. matrix H. NMF has a wide variety of applications, including bioinformatics, chemometrics, communication complexity, machine learning, polyhedral combinatorics, among many others. A longstanding open question, posed by Cohen and Rothblum in 1993, is whether every rational matrix M has an NMF with minimal d whose factors W and H are also rational. We answer this question negatively, by exhibiting a matrix M for which W and H require irrational entries. As an application of this result, we show that state minimization of labeled Markov chains can require the introduction of irrational transition probabilities. We complement these irrationality results with an NP-complete version of NMF for which rational numbers suffice.
Suggested BibTeX entry:
@inproceedings{17CKMSW-SODA,
author = {Dmitry Chistikov and Stefan Kiefer and Ines Marusic and Mahsa Shirmohammadi and James Worrell},
booktitle = {Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA)},
pages = {1290--1305},
publisher = {SIAM},
title = {On Rationality of Nonnegative Matrix Factorization},
year = {2017}
}
|
 |
|
|
|
|
|
|
|
|
|



