Reference:

J. Esparza, S. Römer, and W. Vogler. An improvement of McMillan's unfolding algorithm. In T. Margaria and B. Steffen, editors, Proc. of TACAS'96, number 1055 in Lecture Notes in Computer Science, pages 87–106. Springer-Verlag, 1996.

Abstract:

McMillan has proposed a new technique to avoid the state explosion problem in the verification of systems modelled with finite-state Petri nets. The technique is based on the concept of net unfolding, a well known partial order semantics of Petri nets, later described in more detail under the name of 'branching processes'. The unfolding of a net is another net, usually infinite but with a simpler structure. McMillan proposes an algorithm for the construction of a finite initial part of the unfolding which contains full information about the reachable states. We call such an initial part a finite complete prefix. He then shows how to use these prefixes for deadlock detection. Although McMillan's algorithm is simple and elegant, it sometimes generates prefixes much larger than necessary. In some cases a minimal complete prefix has O(n) in the size of the Petri net, while the algorithm generates a prefix of size 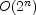. In this paper we provide an algorithm which generates a minimal complete prefix (in a certain sense to be defined). The prefix is always smallerthan or as large as the prefix generated with the old algorithm.

Suggested BibTeX entry:

@inproceedings{ERV96,
    author = {J. Esparza and S. R{\"o}mer and W. Vogler},
    booktitle = {Proc. of TACAS'96},
    editor = {T. Margaria and B. Steffen},
    number = {1055},
    pages = {87--106},
    publisher = {{Springer-Verlag}},
    series = {{Lecture Notes in Computer Science}},
    title = {An Improvement of {McMillan}'s Unfolding Algorithm},
    year = {1996}
}